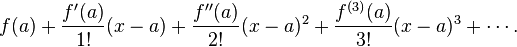이 글은 Dung-Hai Lee 교수의 critical phenomena라는 책(?), 강의노트(?)를 기반으로 스터디한 글입니다.
고수님들 틀린 부분있으면 확실하게 지적해주시기 바랍니다. ('-')/
2.2절 입니다. 전 절에서 썼던 식
) 로 시작해 보도록 하죠.
로 시작해 보도록 하죠.
우선 우리는 온도  일때
일때  즉,
즉,  이므로
이므로  도 0으로 수렴합니다. 그러면 tanh함수를 테일러 급수 전개(talyor expansion)를 할수 있습니다.
도 0으로 수렴합니다. 그러면 tanh함수를 테일러 급수 전개(talyor expansion)를 할수 있습니다.
%5E3%2B%5Cldots)
여기서 <S>를  라고 생각하고 바꿈니다. 스핀의 기대값이나 자기밀도나 같은 값이라고 이야기해도 괜찮겠죠. 여기서
라고 생각하고 바꿈니다. 스핀의 기대값이나 자기밀도나 같은 값이라고 이야기해도 괜찮겠죠. 여기서  는 자발적 자기밀도(spontaneous magnetization)입니다. 그리고
는 자발적 자기밀도(spontaneous magnetization)입니다. 그리고

라고 정의 했었죠.
) 이구요.
이구요.
 로 바꾸면
로 바꾸면
%5E3%20m_0%5E3%20%2B%20%5Cldots)
%5E3%20m_0%5E2%20%2B%20%5Cmathcal%7BO%7D(m_0%5E4)%20%2B%20%5Cldots)
의 형태가 됩니다. 여기서  이므로 4승항 이하로는 제거하도록 하죠. 그리고 나서
이므로 4승항 이하로는 제거하도록 하죠. 그리고 나서  에 대해서 정리하게 되면
에 대해서 정리하게 되면
%7D)
이렇게 됨니다. 우리는  일때를 이야기 했기 때문에 앞에
일때를 이야기 했기 때문에 앞에  항은 1로 가게 되고 뒤에 괄호 안은
항은 1로 가게 되고 뒤에 괄호 안은  이 됨니다. 온도가 임계온도에 가까워지는 경우 값이 0으로 수렴하게 되죠.
이 됨니다. 온도가 임계온도에 가까워지는 경우 값이 0으로 수렴하게 되죠.
 라는 값으로 1장에서 정의 했습니다. 이 양은 0이 될수록 임계온도에 온도가 가까워지게 되는 것이죠.
라는 값으로 1장에서 정의 했습니다. 이 양은 0이 될수록 임계온도에 온도가 가까워지게 되는 것이죠.
결론은  일때
일때  값은 0으로 수렴하게 됨니다. 온도가 임계온도에 가까워지면 자성적 성질이 완전히 사라 지게 되는것이죠.
값은 0으로 수렴하게 됨니다. 온도가 임계온도에 가까워지면 자성적 성질이 완전히 사라 지게 되는것이죠.

라는 식으로 1장에서 이야기한  에서
에서  값을 가지게 됨니다. 실제 실험 값이 0.32 정도 인데요. 조금 멀어보이긴 하지만 그래도 대략적으로 조금은 가까워진거 같네요.
값을 가지게 됨니다. 실제 실험 값이 0.32 정도 인데요. 조금 멀어보이긴 하지만 그래도 대략적으로 조금은 가까워진거 같네요.
다음으로는 임계온도 때에서 외부 자기장 값이 존재할때의 경우를 생각해 보도록 하죠. 여기선 스핀 기대값과 자기장의 관계를 보기위해 이런 접근을 합니다. 그리고 온도가 임계온도이기 때문에  를
를  라고 합니다.
라고 합니다.
)
)
여기서는  이지만 후에
이지만 후에  이기 때문에 외부 자기장 h를 충분히 작다고 생각하고 문제에 접근하면 같은 방식으로 테일러 전개를 할수 있게 됨니다.
이기 때문에 외부 자기장 h를 충분히 작다고 생각하고 문제에 접근하면 같은 방식으로 테일러 전개를 할수 있게 됨니다.
%5E3%2B%5Cldots)
뒤에 5승 이하를 제거 하고 정리하면
%5E3)
%5E%5Cfrac%7B1%7D%7B3%7D%20-%5Cbeta_c%20h%20%3D%3CS%3E)
여기서  라고 가정 하기 때문에 1/3승인 h가 그냥 h보다 훨신 큰 영향을 끼치게 됨니다. (dominant)
라고 가정 하기 때문에 1/3승인 h가 그냥 h보다 훨신 큰 영향을 끼치게 됨니다. (dominant)

이라는 결론이 나옴니다. 이런 경우 임계온도에서 외부 자기장의 세기에 따른 스핀의 기대값이 외부 자기장의 1/3승에 비례한다는 것을 알수 있는데요. 실제 실험값은 1/4.80이니까 대략 비슷한긴 하지만 조금 멀어 보이긴 합니다. 조금씩 평균장 이론(mean-field theory)의 한계가 보이네요.
이제 온도가 임계온도 보다 조금더 높은 부분에서의 상황을 보겠습니다. 여기서  인 상황에서만 생각합니다. 이는 열적 현상에 비해 자기장을 지나치게 세게 가하지 않는 다는 것인데요.. 상자성도 강력한 자기장을 가하게 되면 어느정도 자성을 띄기 때문입니다.
인 상황에서만 생각합니다. 이는 열적 현상에 비해 자기장을 지나치게 세게 가하지 않는 다는 것인데요.. 상자성도 강력한 자기장을 가하게 되면 어느정도 자성을 띄기 때문입니다.
)
<S>=0이기 때문에 위의 식은 다시 쉽게 근사 됨니다.
![<S>\approx\beta(h+ Jz<S>)-\frac{1}{3}\left[\beta(h+ Jz<S>)\right]^3+\ldots](http://eq.springnote.com/tex_image?source=%3CS%3E%5Capprox%5Cbeta(h%2B%20Jz%3CS%3E)-%5Cfrac%7B1%7D%7B3%7D%5Cleft%5B%5Cbeta(h%2B%20Jz%3CS%3E)%5Cright%5D%5E3%2B%5Cldots)
%5Cll1) 이라고 위에서 가정 했기때문에 우선 3승항 이하로는 모두 제거해 보도록 하죠.
이라고 위에서 가정 했기때문에 우선 3승항 이하로는 모두 제거해 보도록 하죠.
)
자 이녀석을 잘 요리해 봅니다.
)

%3CS%3E%5Capprox%20h)
%7D)
온도과 스핀의 기대값은 임계온도보다 조금 높은 부분에서는 이러한 관계를 가집니다. 여기서 스핀의 기대값은 자화율(magnetic susceptibility)와 관계가 있습니다. 상자성을 띄는 상황에서 온도를 얼마나 높여 주느냐에 따라(외부 자기장이 있는 상황에서) 자화가 급격히 낮아지니까요. 강자성에는 스핀이 임계온도에 가까워지지 않으면 모두 한방향을 가르키기 때문에 자화율을 따지는게 의미가 없습니다.
이 식에서는 온도와 자화율은 %5Csim%20T%5E%7B-1%7D) 를 띄는군요. 하지만 실제 실험값은 1.24의 지수를 가진 멱급수(pow-law)를 따름니다. 그래도 조금은 비슷하네요.
를 띄는군요. 하지만 실제 실험값은 1.24의 지수를 가진 멱급수(pow-law)를 따름니다. 그래도 조금은 비슷하네요.
자.. 책에선 이 부분이 가장 논란이 되는 부분인데요. 다음이 1절에서 언급한 헤밀토니안입니다.

처음에 썼던 에너지 연산자(Hamiltonian)을 수정해 줍니다. 전에는 두번 계산(double counting)이 됬덨다고 하네요. 이쪽 공부 해보신 분들은 알겠지만 실제로 각 격자자리(lattices site)들을 지나면서 계산을 하다보면 1번 위치에서 1번 스핀과 2번 스핀 사이에 관계를 계산하고 나서 다시 2번의 위치에서 1번스핀과 2번 스핀의 관계를 또 계산하게 되기때문에 그런 반복된 계산을 제거하기 위해 반으로 나누어 줍니다.
문제는 지금까지 이전의 헤밀토니안으로 이것도 하고 저것도 하면서 잘 써오다가 갑자기 이런식으로 변덕을 주는게 좀 많이 기이하지 않을수 없습니다.

이전 헤밀토니안이 음의 부호가 있기 때문에 저 항을 더해주면 두번 더해준 부분을 제거 할수 있습니다. 책에서 보면은 저 부분의 항은 자화(magnetization)에는 영향을 주지 않는다고 하면서 이르 프리에너지(free energy)에 넣습니다. 이 말 부분도 석연치가 않습니다. 확실히 저 부분이 임계온도에 영향을 주기때문에.. 자화에도 어느정도 영향을 줄텐데 말이죠. 물런 임계온도와의 상대적인 값(t)만을 고려한다면 상관은 없습니다. 이제 슬슬 고통스러운 계산의 시작입니다.

기본적으로 자유에너지(free energy)는 위와 같이 정의 됨니다. 분배함수(partition function)을 적으면,
![f_{mf}=-\frac{k_B T}{N}\ln\lbrace Tr[e^{-\beta\mathcal{H}_{mf}}] \rbrace](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%5Clbrace%20Tr%5Be%5E%7B-%5Cbeta%5Cmathcal%7BH%7D_%7Bmf%7D%7D%5D%20%5Crbrace)
이와 같이 됨니다. 그럼 헤밀토니안을 넣고 계산을 해보죠.
![f_{mf}=-\frac{k_B T}{N}\ln\lbrace \sum_{S_i}\left[e^{\beta \sum_i h_{eff,i}S_i - \frac{J}{2}\beta\sum_{i,j}C_{ij}<S_i><S_j> }\right] \rbrace](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%5Clbrace%20%5Csum_%7BS_i%7D%5Cleft%5Be%5E%7B%5Cbeta%20%5Csum_i%20h_%7Beff%2Ci%7DS_i%20-%20%5Cfrac%7BJ%7D%7B2%7D%5Cbeta%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D%5Cright%5D%20%5Crbrace)
글씨가 작아져서 잘 안보이기 시작하네요.
![f_{mf}=-\frac{k_B T}{N}\ln\lbrace \sum_{S_i}\left[e^{\beta \sum_i h_{eff,i}S_i} e^{- \frac{J}{2}\beta\sum_{i,j}C_{ij}<S_i><S_j> }\right] \rbrace](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%5Clbrace%20%5Csum_%7BS_i%7D%5Cleft%5Be%5E%7B%5Cbeta%20%5Csum_i%20h_%7Beff%2Ci%7DS_i%7D%20e%5E%7B-%20%5Cfrac%7BJ%7D%7B2%7D%5Cbeta%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D%5Cright%5D%20%5Crbrace)
뒤에 두번째 지수(exp)항은 앞에 S_i랑은 관계가 없으므로 로그를 이용해서 제외 시켜 줌니다.
![f_{mf}=-\frac{k_B T}{N}\ln\lbrace \sum_{S_i}\left[e^{\beta \sum_i h_{eff,i}S_i} \right] \rbrace -\frac{k_B T}{N}\ln e^{-\frac{J}{2}\beta\sum_{i,j}C_{ij}<S_i><S_j> }](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%5Clbrace%20%5Csum_%7BS_i%7D%5Cleft%5Be%5E%7B%5Cbeta%20%5Csum_i%20h_%7Beff%2Ci%7DS_i%7D%20%5Cright%5D%20%5Crbrace%20-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%20e%5E%7B-%5Cfrac%7BJ%7D%7B2%7D%5Cbeta%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D)
![f_{mf}=-\frac{k_B T}{N}\ln\lbrace \sum_{S_i}\left[e^{\beta \sum_i h_{eff,i}S_i} \right] \rbrace + \frac{J}{2N} \sum_{i,j}C_{ij}<S_i><S_j> }](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%5Clbrace%20%5Csum_%7BS_i%7D%5Cleft%5Be%5E%7B%5Cbeta%20%5Csum_i%20h_%7Beff%2Ci%7DS_i%7D%20%5Cright%5D%20%5Crbrace%20%2B%20%5Cfrac%7BJ%7D%7B2N%7D%20%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D)
![f_{mf}=-\frac{k_B T}{N}\ln\lbrace \sum_{S_1}\sum_{S_2}\sum_{S_3}\ldots\sum_{S_N}\left[e^{\beta h_{eff,1}S_1}e^{\beta h_{eff,2}S_2}e^{\beta h_{eff,3}S_3}\ldots e^{\beta h_{eff,N}S_N} \right] \rbrace \\+ \frac{J}{2N} \sum_{i,j}C_{ij}<S_i><S_j> }](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cln%5Clbrace%20%5Csum_%7BS_1%7D%5Csum_%7BS_2%7D%5Csum_%7BS_3%7D%5Cldots%5Csum_%7BS_N%7D%5Cleft%5Be%5E%7B%5Cbeta%20h_%7Beff%2C1%7DS_1%7De%5E%7B%5Cbeta%20h_%7Beff%2C2%7DS_2%7De%5E%7B%5Cbeta%20h_%7Beff%2C3%7DS_3%7D%5Cldots%20e%5E%7B%5Cbeta%20h_%7Beff%2CN%7DS_N%7D%20%5Cright%5D%20%5Crbrace%20%5C%5C%2B%20%5Cfrac%7BJ%7D%7B2N%7D%20%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D)

![f_{mf}=-\frac{k_B T}{N}\left[\ln \sum_{S_1}e^{\beta h_{eff,1}S_1}+\ln\sum_{S_2}e^{\beta h_{eff,2}S_2}+\ln\sum_{S_3}e^{\beta h_{eff,3}S_3}+\ldots+\ln \sum_{S_N}e^{\beta h_{eff,N}S_N}\right] \\+ \frac{J}{2N} \sum_{i,j}C_{ij}<S_i><S_j> }](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cleft%5B%5Cln%20%5Csum_%7BS_1%7De%5E%7B%5Cbeta%20h_%7Beff%2C1%7DS_1%7D%2B%5Cln%5Csum_%7BS_2%7De%5E%7B%5Cbeta%20h_%7Beff%2C2%7DS_2%7D%2B%5Cln%5Csum_%7BS_3%7De%5E%7B%5Cbeta%20h_%7Beff%2C3%7DS_3%7D%2B%5Cldots%2B%5Cln%20%5Csum_%7BS_N%7De%5E%7B%5Cbeta%20h_%7Beff%2CN%7DS_N%7D%5Cright%5D%20%5C%5C%2B%20%5Cfrac%7BJ%7D%7B2N%7D%20%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D)
![f_{mf}=-\frac{k_B T}{N}\left[\ln(e^{\beta h_{eff,1}}-e^{-\beta h_{eff,1}})+\ln(e^{\beta h_{eff,2}}-e^{-\beta h_{eff,2}} ) + \ldots +\ln(e^{\beta h_{eff,N}}-e^{-\beta h_{eff,N}})\right] \\ + \frac{J}{2N} \sum_{i,j}C_{ij}<S_i><S_j> }](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cleft%5B%5Cln(e%5E%7B%5Cbeta%20h_%7Beff%2C1%7D%7D-e%5E%7B-%5Cbeta%20h_%7Beff%2C1%7D%7D)%2B%5Cln(e%5E%7B%5Cbeta%20h_%7Beff%2C2%7D%7D-e%5E%7B-%5Cbeta%20h_%7Beff%2C2%7D%7D%20)%20%2B%20%5Cldots%20%2B%5Cln(e%5E%7B%5Cbeta%20h_%7Beff%2CN%7D%7D-e%5E%7B-%5Cbeta%20h_%7Beff%2CN%7D%7D)%5Cright%5D%20%5C%5C%20%2B%20%5Cfrac%7BJ%7D%7B2N%7D%20%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D)
![f_{mf}=-\frac{k_B T}{N}\left[\ln(2\cosh{\beta h_{eff,1}})+\ln(2\cosh{\beta h_{eff,2}})+ \ldots +\ln(2\cosh{\beta h_{eff,N}})\right] \\+ \frac{J}{2N} \sum_{i,j}C_{ij}<S_i><S_j> }](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Cleft%5B%5Cln(2%5Ccosh%7B%5Cbeta%20h_%7Beff%2C1%7D%7D)%2B%5Cln(2%5Ccosh%7B%5Cbeta%20h_%7Beff%2C2%7D%7D)%2B%20%5Cldots%20%2B%5Cln(2%5Ccosh%7B%5Cbeta%20h_%7Beff%2CN%7D%7D)%5Cright%5D%20%5C%5C%2B%20%5Cfrac%7BJ%7D%7B2N%7D%20%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D)
![f_{mf}=\frac{J}{2N} \sum_{i,j}C_{ij}<S_i><S_j> }-\frac{k_B T}{N}\sum_i\ln\left[2\cosh{\beta h_{eff,i}}\right]](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D%5Cfrac%7BJ%7D%7B2N%7D%20%5Csum_%7Bi%2Cj%7DC_%7Bij%7D%3CS_i%3E%3CS_j%3E%20%7D-%5Cfrac%7Bk_B%20T%7D%7BN%7D%5Csum_i%5Cln%5Cleft%5B2%5Ccosh%7B%5Cbeta%20h_%7Beff%2Ci%7D%7D%5Cright%5D)
으로 간단하게 정리가 되네요. 휴... 솔직히 중간에 곱기호를 써서 하면 더 편하지만 이해를 돕기위해서 펼쳤는데 앞으론 간단하게 하겠습니다.
외부 자기장이 균일한 경우에는 전에 봤던대로 간단한 형태로 바꿀수 있습니다. 좀더 복잡한 것을 간단한 것에서 부터 잘 다룰수 있게 됨니다.
![f_{mf}=\frac{Jz}{2}<S>^2 -k_B T\ln\left[2\cosh{\beta \left(h+Jz<S>\right) }\right]](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D%5Cfrac%7BJz%7D%7B2%7D%3CS%3E%5E2%20-k_B%20T%5Cln%5Cleft%5B2%5Ccosh%7B%5Cbeta%20%5Cleft(h%2BJz%3CS%3E%5Cright)%20%7D%5Cright%5D)
i 값과 관계 없이 모든 자리(site)들이 같기 때문에 같은것을 N번 더해주는 것이 되서 N은 소거 됨니다.
 이고 h=0일때는 전부터 언급했던것처럼 물질이
이고 h=0일때는 전부터 언급했던것처럼 물질이  를 가지게 됨니다.
를 가지게 됨니다.
![f_{mf}=\frac{Jz}{2}<S>^2 -k_B T\ln\left[2\cosh{\beta \left(Jz<S>\right) }\right]](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D%5Cfrac%7BJz%7D%7B2%7D%3CS%3E%5E2%20-k_B%20T%5Cln%5Cleft%5B2%5Ccosh%7B%5Cbeta%20%5Cleft(Jz%3CS%3E%5Cright)%20%7D%5Cright%5D)
우선 자유 에너지의 대략적인 모습을 살펴볼 필요가 있는데요. 이를 위해 <S>이 충분히 작다고 가정하고 그때의 자유 에너지를 근사 할수 있습니다.  로 바꾸고 두번째 항을 ln와 cosh항으로 테일러 급수 전개(talyor expansion)를 합니다. 그러면
로 바꾸고 두번째 항을 ln와 cosh항으로 테일러 급수 전개(talyor expansion)를 합니다. 그러면

%3Dx-%5Cfrac%7Bx%5E2%7D%7B2%7D%2B%5Cfrac%7Bx%5E3%7D%7B3%7D%2B%5Cldots)
이런 전개를 적용해서
![f_{mf}=\frac{Jz}{2}<S>^2 -k_B T\ln\left[2 + 2\frac{\beta^2 \left(Jz<S>\right)^2}{2!} }+\ldots\right]](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D%5Cfrac%7BJz%7D%7B2%7D%3CS%3E%5E2%20-k_B%20T%5Cln%5Cleft%5B2%20%2B%202%5Cfrac%7B%5Cbeta%5E2%20%5Cleft(Jz%3CS%3E%5Cright)%5E2%7D%7B2!%7D%20%7D%2B%5Cldots%5Cright%5D)
![\approx \frac{k_B T_c}{2}<S>^2 -k_B T\ln2 -k_B T\ln\left[1 + \frac{\beta^2 \left(Jz<S>\right)^2}{2} }\right]](http://eq.springnote.com/tex_image?source=%5Capprox%20%5Cfrac%7Bk_B%20T_c%7D%7B2%7D%3CS%3E%5E2%20-k_B%20T%5Cln2%20-k_B%20T%5Cln%5Cleft%5B1%20%2B%20%5Cfrac%7B%5Cbeta%5E2%20%5Cleft(Jz%3CS%3E%5Cright)%5E2%7D%7B2%7D%20%7D%5Cright%5D)
![\approx \frac{k_B T_c}{2}<S>^2 -k_B T\ln2 -k_B T\left[\frac{\beta^2 \left(Jz<S>\right)^2}{2} -\frac{\beta^4 \left(Jz<S>\right)^4}{8} \right]](http://eq.springnote.com/tex_image?source=%5Capprox%20%5Cfrac%7Bk_B%20T_c%7D%7B2%7D%3CS%3E%5E2%20-k_B%20T%5Cln2%20-k_B%20T%5Cleft%5B%5Cfrac%7B%5Cbeta%5E2%20%5Cleft(Jz%3CS%3E%5Cright)%5E2%7D%7B2%7D%20-%5Cfrac%7B%5Cbeta%5E4%20%5Cleft(Jz%3CS%3E%5Cright)%5E4%7D%7B8%7D%20%20%5Cright%5D)
![=\frac{k_B T_c}{2}<S>^2 -k_B T\ln2 -k_B T\left[\frac{\beta^2 \left(k_B T_c<S>\right)^2}{2} -\frac{\beta^4 \left(k_B T_c<S>\right)^4}{8} \right]](http://eq.springnote.com/tex_image?source=%3D%5Cfrac%7Bk_B%20T_c%7D%7B2%7D%3CS%3E%5E2%20-k_B%20T%5Cln2%20-k_B%20T%5Cleft%5B%5Cfrac%7B%5Cbeta%5E2%20%5Cleft(k_B%20T_c%3CS%3E%5Cright)%5E2%7D%7B2%7D%20-%5Cfrac%7B%5Cbeta%5E4%20%5Cleft(k_B%20T_c%3CS%3E%5Cright)%5E4%7D%7B8%7D%20%20%5Cright%5D)


T%3CS%3E%5E2%20-k_B%20T%5Cln2%20-%5Cfrac%7Bk_B%7D%7B2%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)T_c%3CS%3E%5E2%20-%5Cfrac%7Bk_B%20T%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%5E4%7D%7BT%5E4%7D%5Cright)%3CS%3E%5E4%7D)
(T_c-T)%3CS%3E%5E2%20-%5Cfrac%7Bk_B%20T%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%5E4%7D%7BT%5E4%7D%5Cright)%3CS%3E%5E4%7D)
%3CS%3E%5E2%20%2B%5Cfrac%7BT%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%5E4%7D%7BT%5E4%7D%5Cright)%3CS%3E%5E4%7D%5Crbrace)
%3CS%3E%5E2%20%2B%5Cfrac%7BT%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E4%7D%5Crbrace)
이것이 계산한 식이고.
%20%3CS%3E%5E2%20%2B%5Cfrac%7BT%7D%7B12%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E4%20%5Crbrace)
이건 책에 있는 식인데요. 확실히 계산한 식이 맞는거 같습니다. 책이 틀렸습니다.
여기서 알수 있는것은 free energy가 우함수(even function)이라는 것입니다. 그리고 온도가 임계온도보다 낮아 지는 경우, 두번째 항이 음수가 되서  이어도 free engergy가 최소가 될수 있습니다. 임계온도가 높을때는 <S>=0 인 경우에만 에너지가 최소가 되죠. 그럼 임계온도보다 낮은 부분에서 free energy를 온도에 변화에 따라 생각해 보도록 하죠. 여기서 중요한건 온도는 임계온도 보다 낮지만
이어도 free engergy가 최소가 될수 있습니다. 임계온도가 높을때는 <S>=0 인 경우에만 에너지가 최소가 되죠. 그럼 임계온도보다 낮은 부분에서 free energy를 온도에 변화에 따라 생각해 보도록 하죠. 여기서 중요한건 온도는 임계온도 보다 낮지만  이기 때문에 온도는 임계온도에 충분히 가까워야 하겠죠?
이기 때문에 온도는 임계온도에 충분히 가까워야 하겠죠?

이런 조건을 만족하는 m을 찻습니다. 이것도 한번 미분한 다음에 <S>의 제곱에 대해서 정리하면 돼는데요. 이건 인내심을 가지고 풀어보도록 하죠.
%20%3CS%3E%20%2B3%5Cfrac%7BT%7D%7B8%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E3%20%5Crbrace%20%3D0)
%20%3CS%3E%20%2B3%5Cfrac%7BT%7D%7B8%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E3%20%5Crbrace%20%3D0)
%20%3CS%3E%20%2B%5Cfrac%7B3T%7D%7B8%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E3%20%20%3D0)
%20%3CS%3E%20%3D%5Cfrac%7B3T%7D%7B8%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E3%20)
%20%20%3D%5Cfrac%7B3T%7D%7B8%7D%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E3%3CS%3E%5E2%20)
%5E3(T-T_c))
제가 계산한 식인데요. 책이랑 달라지기 시작합니다.
이것을 다시 처음 free energy식에 넣어주면은
%3CS%3E%5E2%20%2B%5Cfrac%7BT%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%3CS%3E%5E4%7D%5Crbrace)
%5Cfrac%7B8%7D%7B3T%7D%5Cleft(%5Cfrac%7BT%7D%7BT_c%7D%5Cright)%5E3(T-T_c)%20%2B%5Cfrac%7BT%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%5Cleft(%5Cfrac%7B8%7D%7B3T%7D%5Cleft(%5Cfrac%7BT%7D%7BT_c%7D%5Cright)%5E3(T-T_c)%5Cright)%5E2%7D%5Crbrace)
%5E2%5Cfrac%7B4%7D%7B3T%7D%5Cleft(%5Cfrac%7BT%7D%7BT_c%7D%5Cright)%5E2%20%2B%5Cfrac%7BT%7D%7B8%7D%20%5Cleft(%5Cfrac%7BT_c%7D%7BT%7D%5Cright)%5E4%5Cfrac%7B8%5E2%7D%7B9T%5E2%7D%5Cleft(%5Cfrac%7BT%7D%7BT_c%7D%5Cright)%5E6(T_c-T)%5E2%7D%5Crbrace)
%5E2%5Cfrac%7B4%7D%7B3T%7D%5Cleft(%5Cfrac%7BT%7D%7BT_c%7D%5Cright)%5E2%20%2B%20%5Cfrac%7B8%7D%7B9T%7D%5Cleft(%5Cfrac%7BT%7D%7BT_c%7D%5Cright)%5E2(T_c-T)%5E2%7D%5Crbrace)
%5E2(T_c-T)%5E2%7D%5Crbrace)
(T_c-T)%5E2%7D%5Crbrace)
다음과 같은 결과를 얻게 됨니다.

![f_{mf}=-k_B\left[T\ln 2-\frac{8}{9}\frac{T}{T_c^2}(T-T_c)^2\right] \ \ ;\ T<T_c](http://eq.springnote.com/tex_image?source=f_%7Bmf%7D%3D-k_B%5Cleft%5BT%5Cln%202-%5Cfrac%7B8%7D%7B9%7D%5Cfrac%7BT%7D%7BT_c%5E2%7D(T-T_c)%5E2%5Cright%5D%20%5C%20%5C%20%3B%5C%20T%3CT_c)
책이랑 다르지만 이게 확실히 맞습니다.
임계온도보다 온도가 높을때는 확연하게 스핀항이 없는 것이 확실하게 free energy를 낮추는 것이구요. 임계온도보다 온도가 낮을 때는 스핀의 기대값이 (자화 magnetization)이 확실하게 존재 하므로 두번째 세번째 항이 존재하게 되서 온도가 임계온도보다 낮을때 저런 관계가 존재하게 됨니다. 이 결과에서 우리는 비열(specific heat)를 알수 있게 되는데요.

![C_{h=0}=-T\frac{\partial^2f}{\partial T^2} =k_B\frac{T}{T_c^2}\left[\frac{9}{2}T-3T_c\right] \ \ ;T<T_c](http://eq.springnote.com/tex_image?source=C_%7Bh%3D0%7D%3D-T%5Cfrac%7B%5Cpartial%5E2f%7D%7B%5Cpartial%20T%5E2%7D%20%3Dk_B%5Cfrac%7BT%7D%7BT_c%5E2%7D%5Cleft%5B%5Cfrac%7B9%7D%7B2%7DT-3T_c%5Cright%5D%20%5C%20%5C%20%20%3BT%3CT_c)
이 부분이 책에 나와있는 식입니다. 네.. 저 식은 당연히 틀린 것입니다. 실제 계산은 다르겠죠?
![C_{h=0}=-T\frac{\partial^2 f}{\partial T^2} =-T\frac{8}{9}\frac{\partial f}{\partial T} \left[k_B\frac{1}{T_c^2}(T-T_c)^2+k_B\frac{T}{T^2}2(T-T_c)\right]](http://eq.springnote.com/tex_image?source=C_%7Bh%3D0%7D%3D-T%5Cfrac%7B%5Cpartial%5E2%20f%7D%7B%5Cpartial%20T%5E2%7D%0A%3D-T%5Cfrac%7B8%7D%7B9%7D%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20T%7D%0A%5Cleft%5Bk_B%5Cfrac%7B1%7D%7BT_c%5E2%7D(T-T_c)%5E2%2Bk_B%5Cfrac%7BT%7D%7BT%5E2%7D2(T-T_c)%5Cright%5D)
![=-T\frac{8}{9} k_B\left[ \frac{2}{T_c^2}(T-T_c)+\frac{2}{T_c^2}(T-T_c)+\frac{2T}{T_c^2} \right]](http://eq.springnote.com/tex_image?source=%3D-T%5Cfrac%7B8%7D%7B9%7D%0Ak_B%5Cleft%5B%0A%5Cfrac%7B2%7D%7BT_c%5E2%7D(T-T_c)%2B%5Cfrac%7B2%7D%7BT_c%5E2%7D(T-T_c)%2B%5Cfrac%7B2T%7D%7BT_c%5E2%7D%0A%5Cright%5D)
![=-T\frac{8}{9} k_B\left[ \frac{4}{T_c^2}(T-T_c)+\frac{2T}{T_c^2} \right]](http://eq.springnote.com/tex_image?source=%3D-T%5Cfrac%7B8%7D%7B9%7D%0Ak_B%5Cleft%5B%0A%5Cfrac%7B4%7D%7BT_c%5E2%7D(T-T_c)%2B%5Cfrac%7B2T%7D%7BT_c%5E2%7D%0A%5Cright%5D)
![=-T\frac{8}{9} k_B\left[ \frac{(6T-4T_c)}{T_c^2} \right]](http://eq.springnote.com/tex_image?source=%3D-T%5Cfrac%7B8%7D%7B9%7D%0Ak_B%5Cleft%5B%0A%5Cfrac%7B(6T-4T_c)%7D%7BT_c%5E2%7D%0A%5Cright%5D)
![=-k_B\frac{T}{T_c^2} \left[ \frac{16}{3}T-\frac{32}{9}T_c \right]](http://eq.springnote.com/tex_image?source=%3D-k_B%5Cfrac%7BT%7D%7BT_c%5E2%7D%0A%5Cleft%5B%0A%5Cfrac%7B16%7D%7B3%7DT-%5Cfrac%7B32%7D%7B9%7DT_c%0A%5Cright%5D)
![C_{h=0}=k_B\frac{T}{T_c^2} \left[ \frac{32}{9}T_c-\frac{16}{3}T \right] \ \ \ \ ;T<T_c](http://eq.springnote.com/tex_image?source=C_%7Bh%3D0%7D%3Dk_B%5Cfrac%7BT%7D%7BT_c%5E2%7D%0A%5Cleft%5B%0A%5Cfrac%7B32%7D%7B9%7DT_c-%5Cfrac%7B16%7D%7B3%7DT%0A%5Cright%5D%0A%5C%20%5C%20%5C%20%5C%20%3BT%3CT_c%20)
완성입니다.
두번 미분하는게 좀 까다롭긴 하지만 생각 보다 어려운 것은 아닙니다. 결과값을 실험값과 비교해 보도록 하죠. 실험 값에는
%5E%7B-%5Calpha%7D%20%5C%20%5C%20%5C%20%3B%20T%3ET_c)
%5E%7B-%5Calpha%7D%20%5C%20%5C%20%5C%20%3B%20T%3CT_c)
여기서 A는 그냥 실험적인 상수구요. 비교를 해보니까 비슷한거 같으면서 어떤부분은 많이 다르네요. 평균장 이론의 식만 본다면 비열은 상전이 점에서 연속적이지 않습니다. 우리가 대부분의 온도인 임계온도 위에서만이라도 맞춰본다면  이라고 이야기 할수 있습니다. 실제값인
이라고 이야기 할수 있습니다. 실제값인  과는 조금.. 머네요. 확실히 0과 그보다 조금이라도 큰값은 많이 다른 의미를 가지고 있는 것이니까요.
과는 조금.. 머네요. 확실히 0과 그보다 조금이라도 큰값은 많이 다른 의미를 가지고 있는 것이니까요.
2.2절은 여기 까지네요. 생각 보다 책이 틀린 부분이 많네요. 이제 좀더 어려운 2.3절을 공부해보도록 합니다. !! 힘내시길~!
이 글은 스프링노트에서 작성되었습니다.