좀 오래전에 튜닝르 하기 위해서 소리굽쇠를 구입했습니다.
독일의 위트너 사에서 만든 440Hz의 라(A)음을 내는 녀석이죠. 가격이 2만원입니다.; 사고 나서 후회했습니다..=_=
중요한건 그것보다 저녀석의 성질인데요. 처음 물건을 받았을때 소리굽쇠를 아무리 세게 쳐도 소리가 들리지가 않았습니다. 물런 진동은 느껴지는데 소리가 도무지 들리지가 않았죠. 이상하게 생각되서 귀에 가까이 대니 소리가 작게 들립니다. 황당했습니다. 제가 가한 에너지에 비해 정말 어이없을 정도로 터무니 없이 작은 소리가 나고 있었기 때문이죠. 그리고 이녀석을 이리저리 가지고 놀면서 깨닮은 몇가지 사실들이 있습니다.
- 진동을 준후에 딱딱한 유리나 물체에 가져다가 대면은 큰 소리가 나네요.
-
그냥 진동을 준후에 귀에 가까이 대고 있으면 소리가 오래가더라구요.
- 간단히 이야기해서 에너지가 바로 나오는게 아니라, 작은 소리로 오래오래 나오더라는 거죠
그렇다면.. 왜 그런걸까요.,? 고민하다 얻은 결론은 아주 간단합니다. 네! 쌍극자였습니다. dipole 이란거죠. 그렇다면 왜 이런 현상이 일어나는지 알아보도록 하죠. 저 Y자 모양의 진동자는 단 하나의 방식으로 밖에 진동할수밖에 없습니다. (normal mode가 1개밖에 없습니다. ) 그건 두 쇠가 반대방향으로 움직여서 대칭적으로 움직이는 것입니다. 그렇다면 위상은 어떻게 될까요? 위상은 정반대가 됨니다. 그래서 왼쪽의 쇠가 내는 진동을 오른쪽이 내는 진동이 상쇄시켜서 전체적으로 소리가 작게 들립니다.
그림에는 electric dipole이지만 위상(phase)이 반대인 두개의 음원이라고 생각해도 갇습니다. 저도 처음엔 고민을 많이 했던 부분인데요. 파동도 벡터이고 전기장도 벡터이기때문에 같은 논리로 접근하여도 무관하다는 것을 깨닮았습니다. 물런 위상차를 계산하게 되면 간섭효과가 나타나겠지만 음파의 파장이 너무 길기때문에 (음파의 속도는 330m/s 진동수는 440Hz 이므로 파장은 0.75m가 됨니다.) 그림에서 보았듯이 위상차는
자 그럼 풀어 볼까요. dipole의 potential을 풀어 볼까요. 위의 그림에 답은 있지만 풀어보도록 하죠.
우선 포텐셜은 어떤 지점에 있다고 이야기 할때 저렇게 주어집니다. (전기장이란 벡터장을 스칼라장으로 바꾸어서 품니다. 편리하죠. )
고등학교때 배운 코사인 법칙이죠. 삼각형의 변의 길이를 이렇게 구합니다.
여기서 루트기호를 쒸워주고 거기에다가 r>>d이므로 마지막 제곱하은 제거해버리도록 근사를 합니다.
그 다음 근사에 대해서 설명해 드리도록 하겠습니다.
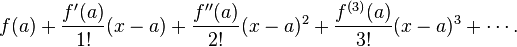
다음과 같은 테일러 근사를 합니다.
여기서 포텐셜을 구해보도록하죠.
이걸 미분을 하면 전체적인 장은
이러한 형태를 가지게 됨니다.
이제 소리굽쇠가 소리가 왜 크지 않은지 알거 같죠? 귀에서 조금만 떨어져도 소리가 급격히 줄어 버립니다.
튜닝에 대해서 말씁드리면.. 소리굽쇠에 진동을 주고 입에 물면 턱을 통해서 고막에 진동을 줍니다. 그리고 나서 기타 4번줄에 7번플렛 하모닉스(3배진동)을 주게 하면 그 음과 굽쇠의 음이 조금 다를경우 맥놀이(beat)가 일어나게 됨니다. 그리고 그 맥놀이를 줄이는 방향으로 조율을 하면 됨니다..
이 글은 스프링노트에서 작성되었습니다.
